Sintesi: Ad oggi, 4 marzo 2020, le rilevazioni pubblicate sul sito della Protezione civile di pazienti positivi al Covid-19 ricoverati con sintomi, di ricoverati in terapia intensiva e di morti continuano a presentare un andamento esponenziale con tempi di raddoppio compresi tra 2 e 2,5 giorni. Se i tempi di raddoppio non cambieranno, si avrà il superamento di 700 pazienti ricoverati in terapia intensiva entro domenica 8 marzo.
Fonte dei dati: Comunicati stampa delle 18:00 della Protezione Civile dal 25/2/2020 al 4/3/2020
http://www.protezionecivile.gov.it/web/guest/media-comunicazione/comunicati-stampa
8/3/2020 ore 2:00: aggiunti confronti con i dati fino al 7 marzo.
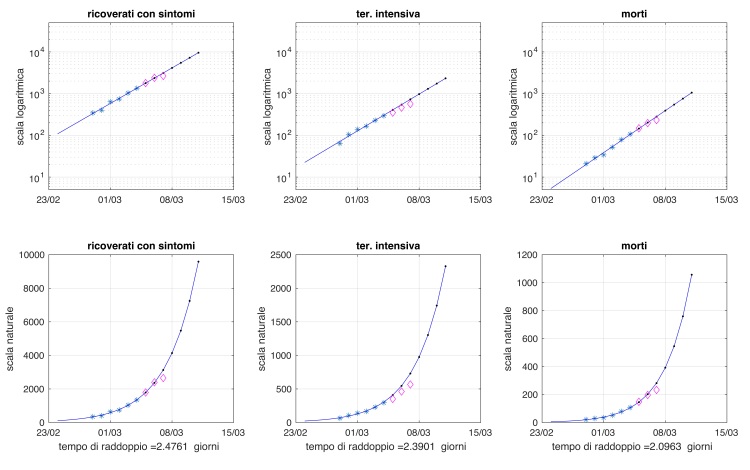
Metodo: Regressione lineare sui dati in scala logaritmica (Fig. 1, sinistra) che, negli ultimi sei giorni, sono ben allineati su una retta. Tale andamento, riportato in scala naturale, corrisponde a curve di crescita di tipo esponenziale (Fig. 1, destra).
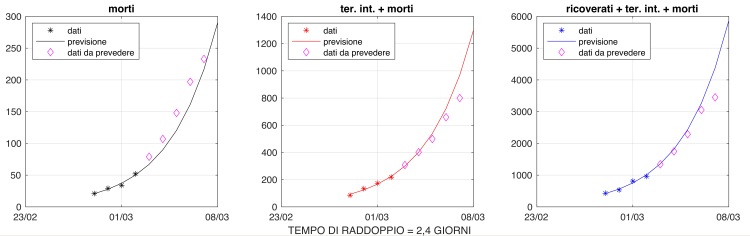
Figura 1: Numero di soggetti positivi al nCoV, ricoverati con sintomi, ricoverati in terapia intensiva, morti: rilevazioni ufficiali dal 28/2 al 4/4 (asterischi blu) e previsioni (pallini neri) nel caso proseguisse la crescita esponenziale. Sinistra: dati in scala logaritmica. Destra: dati in scala naturale.
8 marzo 2020 ore 14:00: aggiunti i dati dei giorni 5-7 marzo (losanghe magenta).
__________
Le tre curve di crescita presentano attualmente i seguenti tempi di raddoppio:
- ricoverati con sintomi: 2,5 giorni
- ricoverati in terapia intensiva: 2,4 giorni
- decessi cumulativi: 2,1 giorni
Per tempo di raddoppio (doubling time) si intende il tempo necessario perché la curva, crescendo, raggiunga il doppio del suo valore di partenza.
Con l’attuale tempo di raddoppio (2,1 giorni), i decessi cumulativi raddoppiano circa ogni due giorni: lunedì 2 marzo erano 52, ieri mercoledì 4 marzo sono saliti a 107. In linea teorica, venerdì 6 marzo potrebbero essere più di 200.
Con l’attuale tempo di raddoppio (2,4 giorni), i ricoveri in terapia intensiva quadruplicano in meno di cinque giorni: il 28 febbraio erano 65, mentre ieri, cinque giorni dopo, sono saliti a 295. In linea teorica, potrebbero superare quota 1.200 entro il 9 marzo.
Validazione: per verificare in che misura la progressione esponenziale si presta a spiegare la crescita dei dati registrati sul sito della Protezione civile, seguendo i suggerimenti di Enrico Bucci ed Enzo Marinari, ho esaminato le seguenti serie storiche:
- D = decessi cumulativi
- G = pazienti gravi = D+ pazienti in terapia intensiva
- R = ricoverati = G + pazienti ricoverati con sintomi.
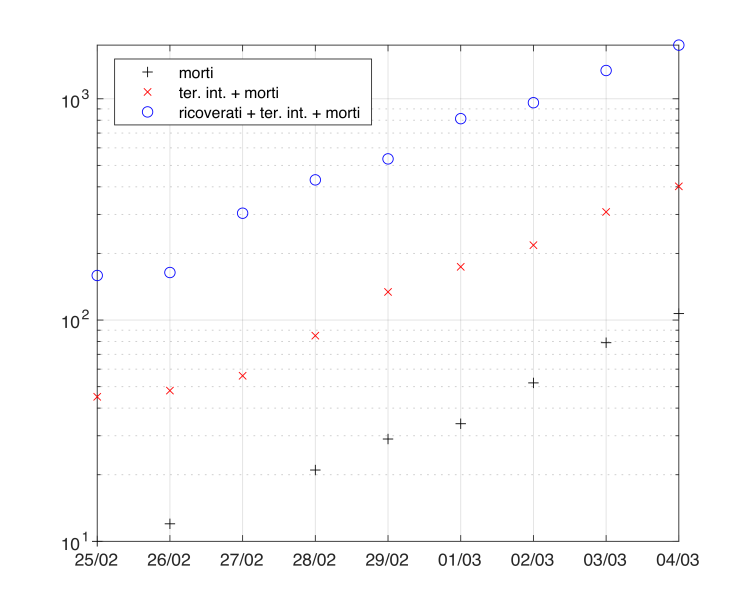
I pazienti positivi al nCoV (oggetto di un precedente post) non sono qui considerati perché, soprattutto dopo il cambio di protocollo relativo all’applicazione dei tamponi (da qualche giorno riservati ai soli sintomatici), forniscono una statistica via via meno affidabile. Riportando i dati D, G, R su una scala logaritmica, si ottiene la seguente figura.
Figura 2: Numero di soggetti D, G, R: rilevazioni ufficiali dal 25/2 al 4/4. Dati in scala logaritmica.
______________
Come si può vedere, le tre serie D, G e R procedono allineate e parallele da diversi giorni. Tale comportamento suggerisce una comune legge di crescita esponenziale. Per verificare se tale ipotesi sia in grado di prevedere, almeno nel breve periodo, l’evoluzione dell’epidemia, si è effettuato il seguente esperimento. Usando i dati D, G, R dei giorni dal 28/2 al 2/3 sono state stimate tre rette con la stessa pendenza e tre diverse intercette, usando per semplicità il metodo dei minimi quadrati. Tali rette sono poi state usate per prevedere i dati D, G, R del 3, 4 e 5 marzo.
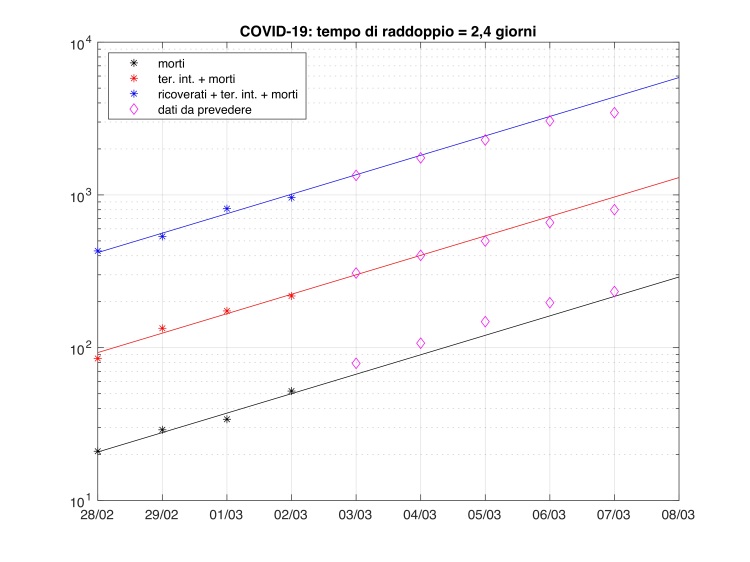
Figura 3: Numero di soggetti D, G, R: rilevazioni ufficiali dal 28/2 al 4/4. Modello lineare con una sola pendenza e tre intercette, stimato usando i dati fino al 2 marzo. I dati del 3 e 4 marzo sono usati a scopo di validazione. Scala logaritmica.
5/3/2020 ore 20:00: aggiunto il dato di validazione del 5 marzo.
8/3/2020 ore 2:00: aggiunti i dati di validazione del 6 e 7 marzo.
____________
Come si vede, non solo le rette seguono bene i dati dal 28/2 al 2/3, ma predicono con ragionevole accuratezza i dati successivi del 3, 4, 5, 6, 7 marzo, a parte una leggera sottostima dei morti. La pendenza comune corrisponde a un tempo di raddoppio di 2,4 giorni, in buon accordo con gli altri tempi di raddoppio ricavati all’inizio dell’articolo. Si ottiene una visualizzazione di comprensione più immediata se si riportano i dati e le curve di previsione sulla scala naturale.
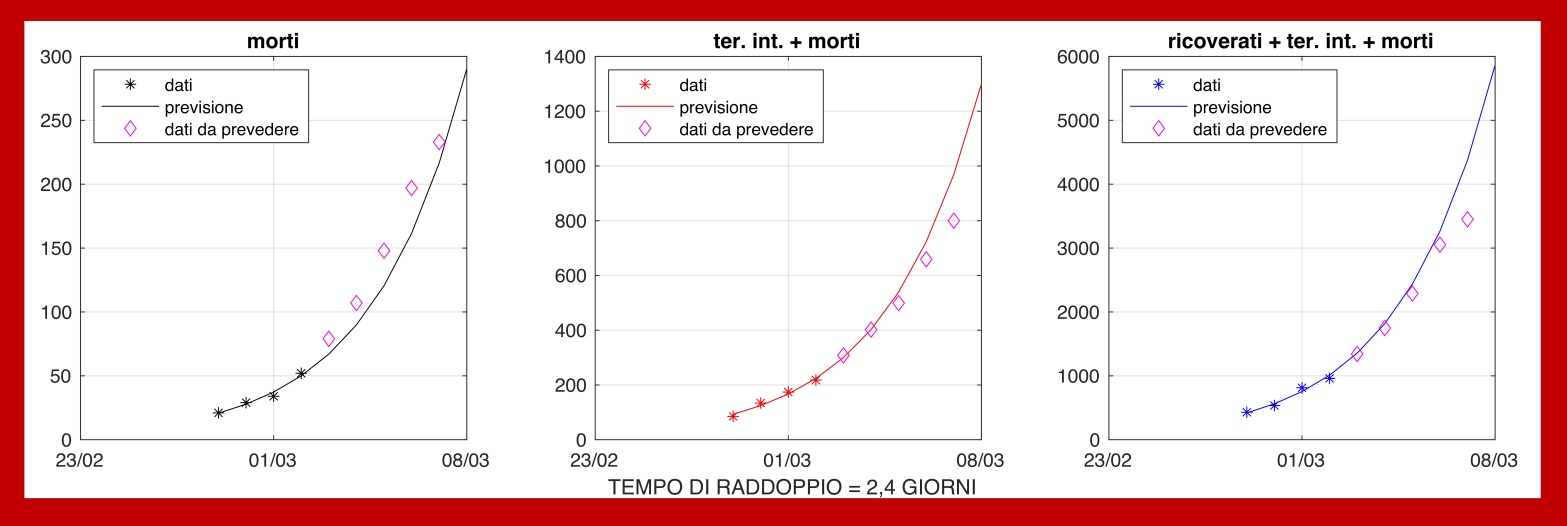
Figura 4: Numero di soggetti D, G, R: rilevazioni ufficiali dal 28/2 al 4/4. Modello lineare con una sola pendenza e tre intercette, stimato usando i dati fino al 2 marzo. I dati del 3 e 4 marzo sono usati a scopo di validazione. Scala naturale.
5/3/2020 ore 20:00: aggiunto il dato di validazione del 5 marzo.
8/3/2020 ore 2:00: aggiunti i dati di validazione del 6 e 7 marzo.
___________
In questa fase iniziale dell’epidemia, il comportamento comune delle serie D, G, R spiega perché anche il dato relativo ai soli pazienti in terapia intensiva (Fig. 1, in mezzo), segua la stessa legge(1). Un discorso analogo vale per i pazienti ricoverati con sintomi, (Fig. 1, in basso).
Previsione: Pur essendo prima o poi destinata ad arrestarsi, la crescita esponenziale sta già mettendo a durissima prova le strutture sanitarie lombarde. Le misure di distanziamento sociale nelle sue varie forme (chiusura di scuole, università, sospensione di eventi pubblici, minor uso di mezzi di trasporto pubblici, telelavoro, etc.) contribuiscono a frenarla. È noto che l’effetto di queste misure, pur non potendo essere immediato perché sconta un ritardo dovuto ai tempi di incubazione, è tanto maggiore quanto più è precoce e rigorosa la loro attuazione. Con un virus che procede a ruota libera, agli inizi della settimana prossima potremmo trovarci a fronteggiare il seguente scenario:
- ricoverati con sintomi: > 3.000
- ricoverati in terapia intensiva: > 700
- decessi cumulativi: > 300
___________
(1) Quelli che secondo la definizione della Protezione civile sono “pazienti in terapia intensiva” coincidono con la differenza G-D, mentre i pazienti ricoverati con sintomi coincidono con la differenza R-G. La differenza tra due funzioni esponenziali con lo stesso esponente è una terza funzione esponenziale che conserva l’esponente comune. Questo spiega perché, in prima approssimazione, tutte le curve esaminate nel post stanno crescendo con tempi di raddoppio relativamente simili, compresi tra 2,1 e 2,5.

Grazie dell’analisi interessante; Mi chiedo due cose..quali sono i C.I. per l’estrapolazione di questi dati? quant’è il power della regressione (spero di non fare affermazioni troppo grossolane…se è così me ne scuso).
Altra domanda, leggevo questa review interessante riguardo proprio ai modelli statistici nelle fasi iniziali dell’epidemia. Potrebbe darmi un commento su questa analisi?
qui il lavoro –> https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5348083/
LikeLike
Sono domande più che legittime dal punto di vista accademico, ma a fronte di un’evoluzione così spiccatamente esponenziale (i grafici semilogaritmici sono inequivocabili), non influenzano il punto principale di questa analisi: c’è una situazione di grave e imminente pericolo per la salute dei cittadini. Un pericolo di due tipi:
1) il collasso delle terapie intensive, insufficienti a salvare i pazienti affetti da insufficienza respiratoria. Come paventato nel mio post di lunedì, pare che la Lombardia sia già arrivata a questo punto:
https://www.lastampa.it/cronaca/2020/03/05/news/coronavirus-in-terapia-intensiva-i-letti-sono-finiti-il-sistema-sanitario-e-al-collasso-1.38550946?fbclid=IwAR1alz3_x62MPqFk58Kj70HF-529nWEkaZcSWLyemIGEqZ8WWXxL1EA7Y0I
2) come effetto collaterale degli sforzi immani tesi a salvare i pazienti colpiti da nCoV, ci sono effetti collaterali importanti per tutti coloro che devono ricorrere alla sanità, sia perché soggetti fragili (anziani, pazienti cronici, critici), sia per patologie improvvise (un infarto o un ictus), tanto più che il personale sanitario sta pagando un prezzo altissimo in termini di contagi e di burn out.
Quando ne saremo fuori, sarà bello discutere di intervalli di confidenza e di power. Fermo restando che per vedere questo TIR in arrivo verso di noi bastavano matita, righello e carta semilogaritmica.
LikeLike
Buongiorno prof, dopo aver letto il suo articolo mi sono imbattuto in quest’altro.
https://m.huffingtonpost.it/entry/cosa-possiamo-predire-con-la-matematica-sul-futuro-dellemergenza-coronavirus_it_5e60ad23c5b6bd126b75eb2e?ncid=other_facebook_eucluwzme5k&utm_campaign=share_facebook
Le conclusioni che vengono tratte qui sembrano vertere su una curva logistica, non esponenziale, come mai? Forse sono stati considerati in modo diverso i dati a disposizione?
LikeLike
Come ho scritto più volte, il numero di pazienti nCoV positivi è ormai affetto da un bias dovuto al cambiamento dei protocollo (tamponi solo per i sintomatici). Stanno pertanto rallentando la crescita rispetto a ricoverati (R), gravi (G) e morti (D). Per monitorare bisogna ormai guardare le tre serie storiche analizzate in questo post. Desumere che stia subentrando la seconda fase della logistica (che segue alla fase esponenziale) senza averla vista, ma trattando i dati osservati come fossero dati usciti da un laboratorio dove viene svolto un esperimento iper-controllato è a dir poco azzardato.
Col procedere del tempo anche le curve R, G, D perderanno affidabilità come indicatori indiretti (e ritardati nel tempo) dell’estensione del contagio. Per esempio, la mancanza di posti letto potrebbe costringere a tenere a casa loro anche i pazienti con sintomi o, comunque, potrebbe ritardare il loro ricovero. Problemi analoghi potrebbero insorgere a causa della carenza dei posti letto in terapia intensiva (vedi notizia sull’utilizzo dei caschi respiratori “una soluzione d’emergenza per affrontare il moltiplicarsi di pazienti con difficoltà respiratorie senza saturare i reparti di terapia intensiva.
“: https://milano.repubblica.it/cronaca/2020/03/02/news/coronavirus_la_regione_lombardia_acquista_i_caschi_respiratori_cosi_i_pazienti_meno_gravi_non_andranno_in_terapia_intensiva-250055125/). L’ultima curva a perdere affidabilità come indicatore indiretto dell’estensione del contagio dovrebbe essere quella dei deceduti (D), anche se, in mancanza di posti letto in terapia intensiva, è inevitabile che salga la mortalità a parità di diffusione dell’epidemia.
LikeLike
Ottimo lavoro
Grazie
LikeLike
A
LikeLike
Ma non si considerano R0, le misure preventive, i guariti, i morti. Facciamo attenzione ad applicare semplici algoritmi matematici…ricordate la diga?
LikeLike
Proprio perché c’è un TIR in arrivo, ho evitato di applicare algoritmi matematici che andassero oltre il prolungamento della sua traiettoria. Ho mostrato solo i dati, i quali, in scala logaritmica, mostrano un evidente profilo rettilineo (il TIR). Se sei nella traiettoria di un TIR lanciato a tutta velocità, un minimo di precauzione suggerisce di scansarsi. Naturalmente può essere che il TIR sterzi all’ultimo momento, ma in questi casi è meglio non fare la verifica sperimentale.
LikeLike
Previsioni ottimistiche. La situazione è molto peggio di come la si cerca di analizzare.
LikeLike
Reblogged this on Blog di Andreas Formiconi and commented:
Analisi seria dei dati (solo in fondo c’è un’affermazione matematica non vera in generale ma solo approssimativamente, e questo non inficia la correttezza dell’analisi).
In due righe, cosa dice questo testo? Che la tendenza degli indicatori del contagio disponibili, ancorché intrinsecamente imperfetti, è sino ad oggi inequivocabilmente esponenziale.
Che vuol dire che un fenomeno ha andamento esponenziale? Che sta esplodendo, a meno che non intervengano fattori esterni a contrastarlo.
Ergo: anche se il rischio personale è piccolo – è enormemente superiore quello di beccarsi un infarto (65000 morti l’anno in Italia) – la responsabilità verso la comunità impone di prendere molto sul serio le misure governative, in primis per non mandare al collasso il sistema sanitario di trattamento delle emergenze.
LikeLike
ottimo lavoro.
LikeLike